킴의 레포지토리
[알고리즘/Python] LeetCode 169. Majority Element 본문
문제
https://leetcode.com/problems/majority-element/?envType=study-plan-v2&envId=top-interview-150
Given an array nums of size n, return the majority element.
The majority element is the element that appears more than ⌊n / 2⌋ times. You may assume that the majority element always exists in the array.
Example 1:
Input: nums = [3,2,3] Output: 3
Example 2:
Input: nums = [2,2,1,1,1,2,2] Output: 2
Constraints:
n == nums.length
1 <= n <= 5 * 10^4
-10^9 <= nums[i] <= 10^9
💡 접근방법
과반수가 넘는 원소는 항상 존재하기 때문에 배열을 정렬했을때 과반수가 넘는 원소는 항상 가운데에 위치합니다.
다음처럼 배열의 길이가 홀수일때 과반을 차지하는 원소는 가장 작거나, 가장 작지도 가장 크지도 않거나, 가장 클 수 있습니다.
1) 배열의 길이가 홀수이면서 과반을 차지하는 원소가 가장 작을때 : [1,1,1,3,4]
2) 배열의 길이가 홀수이면서 과반을 차지하는 원소가 가장 작지도 가장 크지도 않을때: [1,2,2,2,3]
3) 배열의 길이가 홀수이면서 과반을 차지하는 원소가 가장 클때: [1,2,3,3,3]
→ 모두 과반을 차지 하는 원소는 항상 정 가운데(배열의 길이 // 2)에 위치합니다. 과반을 차지하는 원소의 개수는
배열의 길이가 짝수일때 과반을 차지하는 원소는 가장 작거나, 가장 작지도 가장 크지도 않거나, 가장 클 수 있습니다.
1) 배열의 길이가 짝수이면서 과반을 차지하는 원소가 가장 작을때 : [1,1,1,4]
2) 배열의 길이가 짝수이면서 과반을 차지하는 원소가 가장 작지도 가장 크지도 않을때: [1,2,2,2,3,3]
3) 배열의 길이가 짝수이면서 과반을 차지하는 원소가 가장 클때: [1,3,3,3]
→ 모두 과반을 차지 하는 원소는 항상 정 가운데 두 원소(배열의 길이/ 2 혹은 배열의 길이 / 2 - 1)에 위치합니다. n을 배열의 길이라고 할때 과반을 차지하는 원소의 개수는 최소 n / 2 +1 개이므로 (인덱스 0에서 n/2)혹은 (인덱스 n/2 -1부터 n-1)까지 차지하게 됩니다.
따라서, 문제 풀이 과정을 다음과 같습니다.
1. 배열을 정렬합니다.
2. 가운데 원소를 반환합니다. 홀수의 경우 정 가운데 원소, 짝수의 경우 가운데 두 원소 중 오른쪽 원소를 반환합니다.
class Solution(object):
def majorityElement(self, nums):
nums.sort()
mid = len(nums) //2
return nums[mid]문제에서 과반수가 넘는 원소는 항상 존재한다고 하였으므로 원소의 개수가 짝수이면서 최대 빈도수가 n / 2 보다 작거나 같은 경우 즉 [1,2] 혹은 [1,2,2,3]과 같은 경우는 존재하지 않습니다.
✔️시간 복잡도 및 공간 복잡도
시간 복잡도: O(NLogN). 배열을 정렬하기 위한 연산에 O(NLogN) 시간이 소요됩니다.
공간 복잡도: O(1).정렬된 배열을 생성하는 것이 아니라, 배열을 그 자리에서 정렬하기 때문에 별도의 공간이 필요하지 않습니다.
⚒️ 개선1. Counter 라이브러리 사용
단순히 Counter 라이브러리를 사용해서 각 원소별 등장 횟수를 세는 것이 정렬하지 않아도되므로 시간 복잡도 O(N)으로 개선할 수 있습니다.
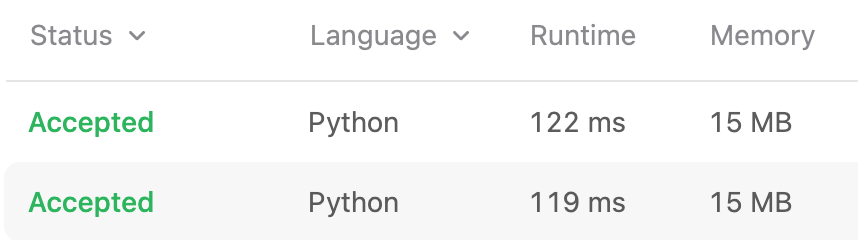
다만, 실제 실행시간은 Counter라이브러리를 사용했을때와 정렬했을때 거의 비슷합니다. 그 이유는 python이 제공하는 정렬 함수를 사용하는 경우 많이 최적화되어있어서 상당히 빠르고(정렬이 필요없는 경우 정렬하지 않음 등), counter를 사용하는 경우 배열을 순회하고도 counter의 item들을 확인해야하기 때문에 N + α의 연산이 발생하기 때문이라고 생각됩니다.
⚒️개선2. Boyer-Moore 과반수 투표 알고리즘 사용
class Solution:
def majorityElement(self, nums: List[int]) -> int:
count = 0
candidate = 0
for num in nums:
if count == 0:
candidate = num
if num == candidate:
count += 1
else:
count -= 1
return candidate✅ 정리
◎ 단순히 배열을 순회하면서 원소별 개수를 세는 방식이 가장 직관적이고 빠를 수도 있다. 더 빠르지만 어려운 알고리즘을 생각해내기 어렵다면, 가장 단순한 방법으로 해결하자.
'study > algorithm' 카테고리의 다른 글
| [알고리즘/Python] LeetCode 121. Best Time to Buy and Sell Stock (0) | 2023.08.25 |
|---|---|
| [알고리즘/Python] LeetCode 189. Rotate Array (0) | 2023.08.25 |
| [알고리즘/Python] LeetCode 80. Remove Duplicates from Sorted Array 2 (0) | 2023.08.24 |
| [알고리즘/Python] LeetCode 27. Remove Duplicates from Sorted Array2 (0) | 2023.08.24 |
| [알고리즘/Python] LeetCode 27.Remove Element (0) | 2023.08.24 |