[알고리즘/python] LeetCode 530. Minimum Absolute Difference in BST - recursive/ iterative(stack) 풀이 포함.

📑 1. 문제 이해

https://leetcode.com/problems/minimum-absolute-difference-in-bst/

Minimum Absolute Difference in BST - LeetCode

이 문제는 이진 탐색 트리(BST)의 서로 다른 두 노드 사이의 값의 차의 최소값을 구하는 문제입니다.  이때 주의할 점은 다음과 같습니다.

- 트리는 빈 트리일 수 없습니다. 노드의 개수가 항상 2개 이상입니다. 항상 루트 노드가 존재하고 level은 최소 1입니다(0부터 시작)

☑️ 테스트케이스

문제에서 주어진 테스트 케이스는 다음과 같습니다. 

 

Example1: root = [4,2,6,1,3]

- 완전 이진 트리입니다.

 

Example2: root =  [1,0,48, null, null, 12, 49]

- 마지막 레벨의 노드들이 오른쪽부터 왼쪽으로 채워져있습니다.

 

추가로 살펴봐야할 테스트 케이스는 다음과 같습니다.

root = [1476, 1054, None, 1, None, None, 215, None, 745]. 다음처럼 연결리스트 형태의 트리입니다.

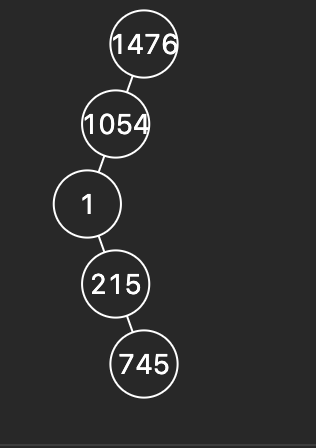
Input으로 주어진 배열이 실제로 함수의 매개변수로 어떻게 들어오는지 알고 싶다면  이전 발행 글 의 배열로 트리 만들기를 참고해주세요.

💡 2. 알고리즘 설계

현재 노드와 가장 거리가 가까운 노드는 왼쪽 서브트리 중 가장 큰 값 혹은 오른쪽 서브트리 중 가장 작은 값이 됩니다. 재귀 함수를 사용해 모든 노드에 대해서 왼쪽 서브트리의 최대값, 오른쪽 서브트리의 최소값을 구한 후 최소 거리를 갱신합니다. 이때 서로 다른 두 노드 사이의 최소값은 1입니다. 따라서 한번이라도 거리가 1인 노드를 발견했다면 함수를 종료시켜 불필요한 연산을 줄일 수 있습니다. 

 

1. 루트 노드에 대해서 재귀 함수를 실행합니다. 

2. 만약 왼쪽 서브트리가 존재한다면 왼쪽 서브트리 중 가장 큰 값을 찾습니다. 그 값과의 거리가 최소 거리보다 작다면 최소 거리를 갱신합니다. 왼쪽 서브트리에 대해서 재귀 함수를 실행합니다.

3. 만약 오른쪽 서브트리가 존재한다면 오른쪽 서브트리 중 가장 작은 값을 찾습니다. 그 값과의 거리가 최소 거리보다 작다면 최소 거리를 갱신합니다. 오른쪽 서브트리에 대해서 재귀 함수를 실행합니다.

4. 최소 거리를 반환합니다.

    
     def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
        min_diff = 10 ** 5 + 1

        def __getMinimumDiffernce(root: Optional[TreeNode]):
            nonlocal min_diff
            if min_diff == 1:
                return
            if root.left:
                maxInLeft = self.getMax(root.left)
                if root.val - maxInLeft < min_diff:
                    min_diff = root.val - maxInLeft
                __getMinimumDiffernce(root.left)

            if root.right:
                minInRight = self.getMin(root.right)
                if minInRight - root.val < min_diff:
                    min_diff = minInRight - root.val
                __getMinimumDiffernce(root.right)

        __getMinimumDiffernce(root)
        return min_dif
        
    def getMax(self, root: Optional[TreeNode]) -> int:
        if root is None:
            return -1
        curr = root
        while curr.right is not None:
            curr = curr.right
        return curr.val

    def getMin(self, root: Optional[TreeNode]) -> int:
        if root is None:
            return -1
        curr = root
        while curr.left is not None:
            curr = curr.left
        return curr.val

시간 복잡도 및 공간 복잡도

시간 복잡도: O(NLogN). 모든 노드에 대해 한번씩 재귀 함수가 실행됩니다. 각 재귀 함수내에서 서브트리를 탐색하는는 것은 최대 O(LogN) 시간 복잡도를 가집니다.  따라서 O(NLogN)이 됩니다.

 

공간 복잡도: O(N). 재귀함수가 총 N번 호출됩니다.

 

⚒️ 3. 최적화

위의 풀이에서는 모든 노드를 여러번 방문하게 되고 매번 getMax(), getMin()을 구하기 위해 이진 탐색 트리의 리프노드들까지 탐색하게 됩니다. 또한, 루트 노드와 오른쪽 서브트리의 가장 작은 값과의 차이는 사실 오른쪽 서브트리의 가장 작은 값과 루트 노드의 값과 같은데 두번 탐색됩니다. 이처럼 위의 풀이에는 중복된 연산이 많습니다. 

 이진 탐색 트리의 중위 탐색 결과는 오름차순이라는 점과 자신보다 작은 값 중 가장 가까운 값 방향으로만 탐색한다면(자신보다 큰 값 중 가장 가까운 값은 탐색하지 않음) 중복 연산을 줄일 수 있습니다.

 다음은 스택과 반복문을 활용한 깊이 우선 탐색 - 중위 순회풀이 코드 입니다.

    def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
        prev = -sys.maxsize
        result = sys.maxsize
        stack = []
        node = root

        while (stack or node) and result != 1:
            while node:
                stack.append(node)
                node = node.left

            node = stack.pop()

            result = min(result, node.val - prev)
            prev = node.val

            node = node.right
        return result

시간 복잡도 및 공간 복잡도

시간 복잡도: O(N). 모든 노드에 대해 한번씩만 스택에 삽입되고 삭제됩니다.

공간 복잡도: O(N). 최악의 경우 스택에  N개가 저장됩니다.

 ⎌ 4. 검토

Example1: root = [4,2,6,1,3]

- 완전 이진 트리입니다. 마지막 반복문에서 스택에서 3이 삭제됩니다. 이때 이전 노드와의 거리는 2로 최소 거리와 같으므로 갱신되지 않습니다. 이후 스택이 비어 반복문이 종료됩니다. 

 

Example2: root =  [1,0,48, null, null, 12, 49]

- 루트노드의 왼쪽 서브트리에 대해서 탐색할때, 0은 자식이 없고 prev = sys.maxsize로 항상 result보다 큽니다. 값이 갱신되지 않습니다. 이후 node = None이 되고 stack= [1]이 됩니다. 1을 스택에서 뺀 후 최소 거리를 1로 갱신합니다. 이후 result = 1이므로 반복문이 실행되지 않습니다.

 

추가로 살펴봐야할 테스트 케이스는 다음과 같습니다.

root = [1476, 1054, None, 1, None, None, 215, None, 745]. 

처음 바깥 반복문 실행 후 결과는 stack = [1467, 1054], node = 215입니다. 두번째 반복문 실행후 왼쪽 자식 노드가 없기 때문에 여전히 stack =[1467, 1054] node = 745입니다. 세번째 반복문 실행후 node = None이 됩니다.  node가 None이라는 것은 서브트리에 대해 탐색이 끝났다는 것으로 루트 노드의 부모 노드에 대해 탐색을 시작합니다. 트리가 연결리스트 형식인 경우에도 방문한 결과가 중위 순회가 됩니다.

---

✅ 정리

◎ 깊이 우선 탐색(DFS)의 경우 반복문과 스택을 활용한 버전과 재귀 버전이 있습니다.

◎ 깊이 우선 탐색의 중위 순회 결과는 오름차순입니다.

◎ 자신과 가장 가까운 거리의 노드를 찾기 위해서는 오름차순 정렬된 결과가 필요합니다.

◎ 스택을 활요한 DFS 버전을 알아두면 응용하기 좋습니다.