킴의 레포지토리
[알고리즘/Python] LeetCode 35. Search Insert Position 본문
📑 1. 문제 이해
https://leetcode.com/problems/search-insert-position/?envType=study-plan-v2&envId=top-interview-150
Search Insert Position - LeetCode
Can you solve this real interview question? Search Insert Position - Given a sorted array of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order. You must w
leetcode.com
이 문제는 오름차순으로 정렬된 배열에서 target을 삽입할 위치를 찾는 것입니다. 이때, 중복된 원소는 존재하지 않지만, target과 그 값이 일치하는 원소는 존재할 수 있습니다. target을 삽입할 위치는 target보다 크거나 같은 원소 중 가장 왼쪽에 있는(작은) 인덱스를 찾는 문제입니다. 배열의 원소가 오름차순으로 정렬되어 있고, O(LogN) 복잡도를 가지도록 해야한다는 점에서 이진탐색을 떠올릴 수 있습니다. 또 조건을 만족하는 원소들 중 가장 작은 인덱스를 찾는 문제로 parametric search 알고리즘을 활용할 수 있습니다.
☑️ 테스트케이스
문제에서 주어진 테스트 케이스는 다음과 같습니다.
1) Example 1: nums=[1,3,5,6] , target = 5
- target과 일치하는 원소가 존재한다.
2) Example 2: nums=[1,3,5,6] , target = 2
- target과 일치하는 원소가 존재하지 않는다.
3) Example 3:nums=[1,3,5,6] , target = 7
- 모든 원소가 target보다 작다.
추가해서 생각해볼 테스트 케이스는 다음과 같습니다.
4) nums=[1,3,5,6] , target = -2
- 모든 원소가 target보다 크다.
5) nums=[1], target = 1
- 배열의 길이가 1이다.
💡 2. 알고리즘 설계
이진 검색을 통해 범위를 반으로 줄여가면 탐색을 합니다. 이때 target보다 크거나 같은 원소라면 그 인덱스를 result라는 변수에 기억해두고 탐색 범위를 mid를 기준으로 왼쪽 범위로 수정합니다. 다시 한번 값이 target보다 크거나 작은 원소를 만나면 result 값을 갱신합니다. 왜냐하면 한번 target보다 크거나 같은 값을 발견하면 그 탐색범위가 그보다 왼쪽으로 한정되기 때문에 나중에 target보다 크거나 같은 값이 등장한다면 그 인덱스는 항상 이전 인덱스보다 작기 때문입니다. 이를 통해 target보다 크거나 같은 원소들 중 가장 작은 인덱스를 찾을 수 있습니다.
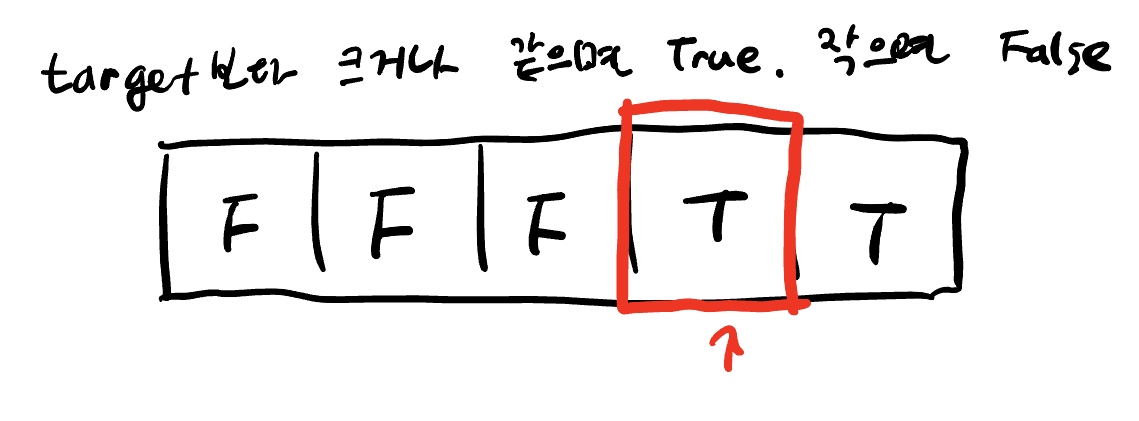
우리가 찾아야하는 인덱스를 그림으로 나타내면 다음과 같습니다. 특정 인덱스의 원소가 target보다 크거나 같으면 True, 작으면 False라고 했을때, 계속 False이다가 처음 target보다 크거나 같은 원소를 만나면 그 이후는 모두 그 원소보다 크므로 계속 True가 됩니다. 우리는 True인 원소들 중 가장 왼쪽의 인덱스를 찾아야합니다.
1. 탐색범위를 나타내는 lo, hi가 배열의 시작과 끝을 가리키도록 합니다. 첫 탐색의 탐색 범위는 전체가 됩니다.
2. 탐색 범위의 가운데 원소 값을 target과 비교합니다.
- 탐색 범위의 길이가 홀수라면 정가운데 원소, 탐색 범위의 길이가 짝수라면 가운데 두 원소중 앞쪽 원소를 기준으로 합니다.
- target보다 크거나 같다면 그 인덱스 mid를 result에 기록합니다. 또, 탐색범위를 mid보다 왼쪽 범위로 한정합니다.
- target보다 작다면 탐색 범위를 mid보다 오른쪽 범위로 한정합니다.
3. lo, hi 포인터가 역전되지 않는동안 이진 탐색을 계속합니다. while문이 끝나게 되면 모든 원소의 값이 비교된 것입니다.
4. 만약 result가 None이 아니라면 최소한 하나의 원소가 target보다 크거나 같다는 것으로 그 인덱스를 반환합니다. result가 None이라면 모든 원소가 target보다 작다는 것으로, 배열의 길이를 반환합니다.(target을 배열의 끝에 추가한다는 뜻입니다.)
def searchInsert(self, nums: List[int], target: int) -> int:
lo, hi = 0, len(nums) - 1
result = None
while lo <= hi:
mid = (lo + hi) // 2
if nums[mid] >= target:
result = mid
hi = mid - 1
else:
lo = mid + 1
return result if result is not None else len(nums)이때 주의할점은 마지막 값 반환시 result값이 존재하는 경우를 체크하기 위해 다음과 같이 result 자체를 if 조건문에서 검사하면 안된다는 것입니다.
return result if result else len(nums)배열의 모든 원소가 target보다 큰 경우 result는 0이 되는데 0도 Falsy로 처리되어 len(nums)가 반환되기 때문입니다.
시간 복잡도 및 공간 복잡도
시간 복잡도: O(LogN)
- 이진 탐색은 범위를 반으로 줄여가며 탐색하는 것으로 최대 LogN번 while문이 반복됩니다.
공간 복잡도: O(1)
- 추가 공간이 필요하지 않습니다.
✅ 정리
◎ 정렬된 배열에서 조건을 만족하는 최솟값, 최대값을 구하는 문제의 경우 이진검색을 응용한 parametric search를 떠올린다.
'study > algorithm' 카테고리의 다른 글
| [알고리즘/Python] LeetCode 74. Search a 2D Matrix (0) | 2023.08.28 |
|---|---|
| [알고리즘/Python] LeetCode 209. Minimum Size Subarray Sum (0) | 2023.08.28 |
| [알고리즘/Python] LeetCode 167. Two Sum 2 - Input Array Is Sorted (0) | 2023.08.28 |
| [알고리즘/Python] LeetCode 125. Valid Palindrome (1) | 2023.08.28 |
| [알고리즘/Python] LeetCode 55. Jump Game (0) | 2023.08.25 |